Schwamm drüber!

In einer der letzten Stunden habe ich mit einer 11. Klasse ChatGPT im Matheunterricht ausprobiert. Die Fragestellung für die Stunde lautete: "Wie kann man ChatGPT zum Lernen für Mathe nutzen? Und speziell für Differenzialrechnung?"

Schülerideen waren:

• Rechenaufgaben stellen lassen
• Rechenaufgaben lösen
• Fachbegriffe erklären lassen
• einen Lernplan zur Vorbereitung auf eine Klausur/auf die Abiturprüfung erstellen

Danach ging es ans Ausprobieren. Die Prompts und Ausgaben wurden anschließend vorgestellt und beurteilt. Wesentliche Probleme waren für die Schülerinnen und Schüler dank monatelanger intensiver Auseinandersetzung mit der Differenzialrechnung offensichtlich: Die Matheaufgaben waren teilweise sehr einseitig ("Bestimme die Ableitung", "Berechne die Extrempunkte"), es gab viele Fehler in den Lösungen (konstanter Summand im Funktionsterm taucht auch in der Ableitung auf, trotz mehrfacher Promptanpassung) und in den Erklärungen wurden Begriffe verwendet, die deutlich über das Kerncurriculum hinausgehen.

Banal ist aus meiner Sicht die Erkenntnis, dass man zur angemessenen Nutzung von ChatGPT deutliches Hintergrundwissen benötigt, um die Ergebnisse zu beurteilen und die Prompts anzupassen. Ebenso wenig überraschend war, dass ChatGPT als Neuronales Netz, das Sprache imitiert, kein Mathe "kann" (dafür gibt es Taschenrechner und Wolfram Alpha). Schön war, das mit den Schülern zu analysieren und so das gesamte Thema zu wiederholen (statt nur Rechenaufgabenzu lösen).

Ich nehme nun ein Werkzeug mit, dass mir für das neue Schuljahr jede Menge Material zur Fehlersuche generiert.

Wie sieht es bei euch im Lehrerpult im Klassenraum aus? Gähnende Leere, Ablage für diverse Zettel oder wohlsortiertes Arbeitsfach?

Während es Schulen mit Lehrerraumprinzip gibt, an denen jede Lehrkraft ihren (Fach-)Raum hat und die Schüler zwischen den Räumen wandern, laufe ich an meiner Schule von Klassenraum zu Klassenraum mit allen Materialien im Gepäck. Um mir wenigstens im Klassenraum der eigenen Klasse dies zu ersparen, habe ich im Lehrerpult eine Box mit den wichtigsten Utensilien untergebracht, die von anderen Lehrkräften in dieser Klasse mitgenutzt werden dürfen. Diese Box beinhaltet:

• ein Locher (das allerallerwichtigste Utensil)
• Pinnadeln (das zweitallerwichtigste Utensil, es gibt ja immer etwas aufzuhängen)
• Malerkrepp (nicht nur zum Aufhängen von Plakaten)
• Klebenotizzettel
• Notizzettel im Klassensatz (für Abstimmungen wie die Klassensprecherwahl)
• eine Schere
• ein Klebestift
• Tesafilm
• Jonglierbälle (für Klassenspiele oder einfach zum Kopfrechnen)
• bunte Servietten (früher für die Geburtstagskerze, jetzt als Unterlage für Diverses)
• Klebemagnete (halten aber nicht wirklich gut und werden wohl als nächstes rausfliegen)

Im Laufe des letzten Schuljahres haben ihren Weg in die Box gefunden, da sie offenbar niemandem gehörten:

• fünf Buntstifte
• ein Bleistift
• zwei angekaute Radiergummis
• ein Tintenkiller

Zu Kreidetafelzeiten hatte ich auch immer eine Schachtel Kreide im Pult. Die jetzigen Whiteboardmarker sind immer wieder aus dem Pult verschwunden, außerdem habe ich davon immer welche in der Tasche, daher lege ich keine mehr ins Pult.

Und bei euch so?

Ich mag Spiele, deren Spielregeln variiert werden können. Damit lassen sich diese Spiele nicht nur für genau eine Unterrichtssituation einsetzen.

Das folgende Spiel habe ich mir selbst überlegt, ich nenne es "Froschteich". Und der sieht so aus (mit Excalidraw erstellt):

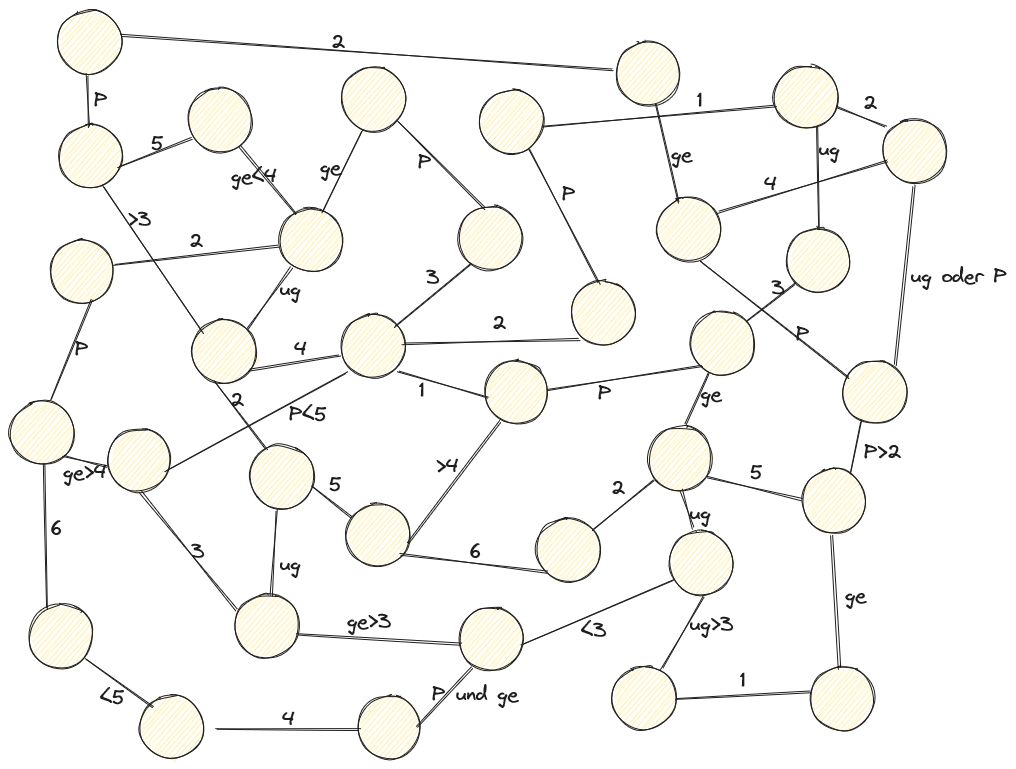
Man benötigt:

• ein Spielbrett (der Froschteich, siehe Bild)
• einen Würfel
• je Spieler einen Stift (verschiedene Farben).

Jeder Spieler markiert zu Beginn mit einem Stift ein Seerosenblatt (die Kreise), auf dem er startet (jedoch keine zwei Frösche auf einem Blatt). Nun wird reihum (z.B. im Uhrzeigersinn) mit einem Würfel gewürfelt und dadurch zu einem anderen Seerosenblatt springen. Die Linien geben an, zu welchem Seerosenblatt man springen kann. Die Beschriftung gibt wiederum an, unter welcher Bedingung man springen kann:

• 1,2,3,4,5,6: Die gewürfelte Zahl ist 1 bzw. 2 bzw. 3 etc.
• P: Die gewürfelte Zahl ist eine Primzahl
• ge: Die gewürfelte Zahl ist gerade
• ug: Die gewürfelte Zahl ist ungerade
• <x bzw. >x: Die gewürfelte Zahl ist kleiner bzw. größer als die Zahl x
• "und" bzw. "oder": entsprechen den logischen Verknüpfungen UND (beide Bedingungen müssen erfüllt sein) bzw. ODER (mindestens eine der beiden Bedingungen müssen erfüllt sein)

Springt man entlang eines Pfades, markiert man ihn mit seinem Stift. Da verschiedene Frösche entlang dieses Pfades springen können, kann ein Pfad auch mit mehreren Stiften markiert werden (es empfiehlt sich, verschiedene Farben zu verwenden und die Spielerzahl auf max. 4 zu begrenzen).

Wer es geschafft hat im Kreis zu springen, also über verschiedene Pfade wieder am Startpunkt anzukommen, kann sich die Weglänge als Punkte aufschreiben und sich ein neues Seerosenblatt als neuen Startpunkt aussuchen. Wenn alle Pfade übersprungen worden sind, endet das Spiel. Gewonnen hat, wer die meisten Punkte erreicht hat.

Das Spielfeld kann man vereinfachen, indem nur Zahlen an den Pfaden stehen, oder noch weiter ausbauen, indem mit zwei Würfeln gewürfelt wird und die Ereignisse entsprechend komplexer gestaltet werden können.

Im Matheunterricht kann das Spiel z.B. mit Baumdiagrammen ausgewertet werden: Welcher Pfad ist (bei gleicher Wurfzahl) wahrscheinlicher? Wie groß ist die Wahrscheinlichkeit, den kürzesten Rundweg ohne Aussetzen (wenn man mal nicht springen kann) zu erwürfeln? (Edit: Und ganz schnell ist man hier bei Markovketten.)

Im Informatikunterricht kann das Spiel entsprechend programmiert werden, so dass eingefärbte Pfade automatisch auf Kreise überprüft und der Punktestand aktualisiert wird. Auch könnte ausgewählt werden, ob man gegen einen anderen Mitspieler oder gegen den Computer spielen möchte.

Das Spiel ist noch im Werden. Ideen und Verbesserungsvorschläge nehme ich gern entgegen.