Schwamm drüber!

Seit zwei Jahren läuft nun das Pflichtfach Informatik. Und es ist so dringend nötig! Nicht nur wegen des Einblicks in den Rechner oder ins Programmieren. Das ist zwar auch sehr beeindruckend und bei Letzterem auch sehr kreativ (außer man googelt oder KI-t [gibts das als Verb?] Lösungsskripte).

Die erste Stunde beginnt aber viel banaler, eigentlich gehört es in den Bereich "Medienbildung": Die Schüler:innen sollen fürs Fachmaterial Ordner und Unterordner erstellen und dann die ausgeteilten Dateien abspeichern und nach Vorgabe umbenennen. Und ich bin immer wieder überrascht, wie viel Zeit dies beansprucht. Wir reden hier von Klasse 9 und 10, die bereits Erfahrung im Umgang mit Dateien haben sollten, schließlich mussten sie schon Präsentationen oder Texte digital abgeben. Aber offenbar nicht mit einem vorgegebenen Dateinamen.

Für das Hochladen von Dateien im Aufgabenmodul ist dies auch nicht unbedingt notwendig. Die Dateien kann man ja mit Klick auf den Schülernamen öffnen. Wenn man sie herunterlädt, werden sie in Ordnern mit Schülernamen gespeichert. Und die Schüler:innen brauchen nur ihre Datei hochladen, wo auch immer und unter welchem Namen auch immer sie gespeichert ist. Also warum dann so viel Tantam?

Es geht darum, den Rechner oder das Tablet oder das Smartphone als Werkzeug zu verstehen. Im Idealfall beherrscht das Werkzeug nicht mich, sondern ich beherrsche das Werkzeug. Ich kontrolliere, was ich wann, wo und wie speichere. Wenn das Gerät mir dies nicht ermöglicht, dann ist es für mich unbrauchbar.

Jedes Gerät und jede App speichert unterschiedlich. Das geht mit dem Speicherort los und geht beim Dateinamen weiter - vom Dateiformat ganz zu schweigen! Dabei entstehen dann so unhandliche Dateinamen wie "Scratch-Projekt (1)(4).sb3", bei denen man nicht weiß, ob sich dahinter nun das Pacman-Spiel oder der Rasenmähroboter befindet oder ob es sich um die erste, unvollständige Version oder die letzte, gründlich überarbeitete und fehlerbereinigte Version handelt.

Beim Hochladen der Datei stellt sich dann die Frage, wo die Datei eigentlich gespeichert ist. Im Download-Ordner sucht man nicht unbedingt als erstes (dort werden z.B. im Browser entwickelte Scratch-Dateien allerdings gespeichert). Da wäre es doch sinnvoller, alle wichtigen Dateien aller Apps dort zu speichern, wo man sie auch wiederfindet, also im eigenen Ordner.

Im Idealfall speichern die Schüler:innen also ihre Dateien in den dafür vorgesehehen Ordnern und Unterordnern und benennen ihre Dateien nach meinen Kriterien und haben nach dem Inforamtikunterricht die Wahl, ob sie die Kriterien beibehalten oder für sich anpassen oder weiterhin auf die Vorgaben des Geräts setzen.

In der Realität erhält man von mindestens 1/3 der Schüler:innen das gesamte Halbjahr lang Dateien der Form "Dokument1.docx" oder "Scratch-Projekt (1)(4).sb3". Und es war dann garantiert nicht die richtige oder endgültige Abgabe.

Ich mag Spiele, deren Spielregeln variiert werden können. Damit lassen sich diese Spiele nicht nur für genau eine Unterrichtssituation einsetzen.

Das folgende Spiel habe ich mir selbst überlegt, ich nenne es "Froschteich". Und der sieht so aus (mit Excalidraw erstellt):

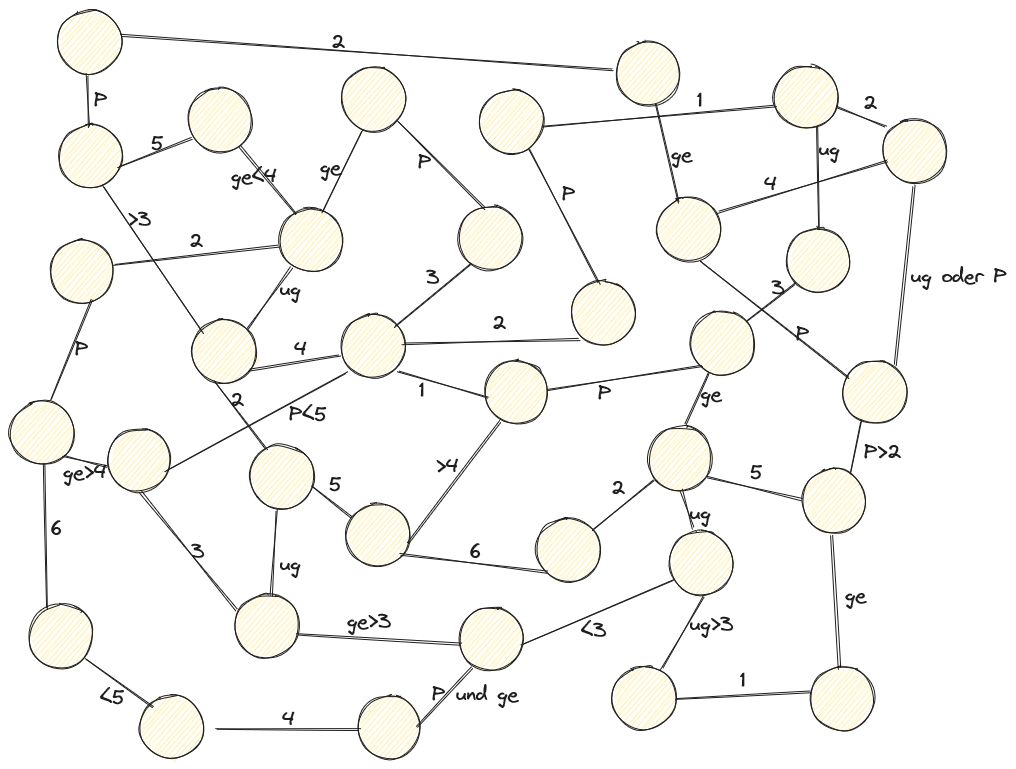
Man benötigt:

• ein Spielbrett (der Froschteich, siehe Bild)
• einen Würfel
• je Spieler einen Stift (verschiedene Farben).

Jeder Spieler markiert zu Beginn mit einem Stift ein Seerosenblatt (die Kreise), auf dem er startet (jedoch keine zwei Frösche auf einem Blatt). Nun wird reihum (z.B. im Uhrzeigersinn) mit einem Würfel gewürfelt und dadurch zu einem anderen Seerosenblatt springen. Die Linien geben an, zu welchem Seerosenblatt man springen kann. Die Beschriftung gibt wiederum an, unter welcher Bedingung man springen kann:

• 1,2,3,4,5,6: Die gewürfelte Zahl ist 1 bzw. 2 bzw. 3 etc.
• P: Die gewürfelte Zahl ist eine Primzahl
• ge: Die gewürfelte Zahl ist gerade
• ug: Die gewürfelte Zahl ist ungerade
• <x bzw. >x: Die gewürfelte Zahl ist kleiner bzw. größer als die Zahl x
• "und" bzw. "oder": entsprechen den logischen Verknüpfungen UND (beide Bedingungen müssen erfüllt sein) bzw. ODER (mindestens eine der beiden Bedingungen müssen erfüllt sein)

Springt man entlang eines Pfades, markiert man ihn mit seinem Stift. Da verschiedene Frösche entlang dieses Pfades springen können, kann ein Pfad auch mit mehreren Stiften markiert werden (es empfiehlt sich, verschiedene Farben zu verwenden und die Spielerzahl auf max. 4 zu begrenzen).

Wer es geschafft hat im Kreis zu springen, also über verschiedene Pfade wieder am Startpunkt anzukommen, kann sich die Weglänge als Punkte aufschreiben und sich ein neues Seerosenblatt als neuen Startpunkt aussuchen. Wenn alle Pfade übersprungen worden sind, endet das Spiel. Gewonnen hat, wer die meisten Punkte erreicht hat.

Das Spielfeld kann man vereinfachen, indem nur Zahlen an den Pfaden stehen, oder noch weiter ausbauen, indem mit zwei Würfeln gewürfelt wird und die Ereignisse entsprechend komplexer gestaltet werden können.

Im Matheunterricht kann das Spiel z.B. mit Baumdiagrammen ausgewertet werden: Welcher Pfad ist (bei gleicher Wurfzahl) wahrscheinlicher? Wie groß ist die Wahrscheinlichkeit, den kürzesten Rundweg ohne Aussetzen (wenn man mal nicht springen kann) zu erwürfeln? (Edit: Und ganz schnell ist man hier bei Markovketten.)

Im Informatikunterricht kann das Spiel entsprechend programmiert werden, so dass eingefärbte Pfade automatisch auf Kreise überprüft und der Punktestand aktualisiert wird. Auch könnte ausgewählt werden, ob man gegen einen anderen Mitspieler oder gegen den Computer spielen möchte.

Das Spiel ist noch im Werden. Ideen und Verbesserungsvorschläge nehme ich gern entgegen.

Im Matheunterricht der 9. Klasse stehen die Vierfeldertafeln an. Ich mag das Thema, weil es viele Anknüpfungspunkte zur Lebenswelt der Schüler:innen hat. Da gibt es tendenziöse Zeitungsartikel (die Zahlen stimmen durchaus, aber sie beschreiben nicht die Gesamtsituation), medizinische und psychologische Tests (mit ersterem haben nun alle hinreichend Erfahrung) und zweifelhafte Zeugenaussagen.

Eine Aufgabe zur Zeugenaussage geht knapp zusammengefasst so: In einem Ort gibt es zwei Taxifirmen, die Grünen und die Blauen. Von den Grünen gibt es z.B. 80, von den Blauen 20. Eines Tages baut eins der Taxis einen Unfall und ein Zeuge beobachtet dies. Er sagt aus, dass er ein blaues Taxi gesehen hat. Ein Sehtest ergibt, dass er zu 80% mit seiner Farberkennung richtig liegt. Wie sollte die Schadenssumme verteilt werden, wenn beide Taxiunternehmer bereit sind, diese zu übernehmen? (Offenbar trauen beide Unternehmen ihren Fahrern nicht übern Weg…)

An sich ist das schon eine schöne Aufgabe, geht sie doch auf die Bedeutung einer Zeugenaussage und ihre Glaubwürdigkeit ein. Vor Gericht sind aufgrund von fehlenden Kenntnissen über die bedingte Wahrscheinlichkeit schon unglaublich große Fehler passiert.

Nun werden zunehmend Überwachungskameras eingesetzt und automatisch ausgewertet. Da wäre es doch naheliegend, die menschliche Aussage durch ein Ergebnis der Bilderkennung zu ersetzen. Aus den Farben wird dann z.B. groß/klein (die Minis und die Maxis), die Bilderkennung liegt dann entsprechend 80% richtig. Wie sicher ist dann, dass es sich um ein Maxi-Taxi handelt? Eine Beurteilung des Einsatzes von Bilderkennung führt zu einer recht spannenden Diskussion.

Und der Bezug zur Informatik ist auch gleich da. Was sind Merkmale, an denen ein Mini- oder Maxi-Taxi erkannt werden kann? Wie wurde es trainiert? Welche Fehler können dabei auftreten (z.B. indem ein Mini-Taxi immer neben einem Haus steht, könnte ein Maxi-Taxi dadurch fälschlicherweise als Mini-Taxi erkannt werden, weil es nun zufällig neben einem Haus steht.)

Als Abschluss kann man selbst ein neuronales Netz mittrainieren:  https://quickdraw.withgoogle.com/
In 19 Sekunden muss zu einem vorgegebenem Begriff ein Bild gezeichnet werden. Erkennt die KI das Bild, gibt es einen Punkt. Am Ende kann man auch auf jedes Bild klicken und sehen, wie andere den Begriff gezeichnet haben.

Edit: Ein unglaublich spannender Einblick in Fehlurteile und die dahinterliegende Mathematik gibt es in "Bayes and the Law".

Um Netzwerke zu simulieren, war bisher Filius unübertroffen. Nun gibt es eine weitere vielversprechende Simulation: "WebNetSim" von Michael Hielscher. Sie führt Schritt für Schritt und sehr anschaulich durch den Aufbau und die Funktionsweise eine Netzwerkes. Zusätzlich kann kollaborativ an einem Netzwerk gearbeitet werden. (Tipp von @beatdoebli)

Von Michael Hielscher stammt auch der didaktische Textgenerator "SoekiaGPT", mit dem man die Funktionsweise von Textgeneratoren wie ChatGPT erkunden kann. Nicht nur für den Informatikunterricht nützlich, sondern zum Beispiel als Anwendung von bedingten Wahrscheinlichkeiten im Matheunterricht (Klasse 9-13).